Separable extension
In modern algebra, an algebraic field extension  is a separable extension if and only if for every
is a separable extension if and only if for every 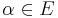 , the minimal polynomial of
, the minimal polynomial of  over F is a separable polynomial (i.e., has distinct roots).[1] Otherwise, the extension is called inseparable. There are other equivalent definitions of the notion of a separable algebraic extension, and these are outlined later in the article.
over F is a separable polynomial (i.e., has distinct roots).[1] Otherwise, the extension is called inseparable. There are other equivalent definitions of the notion of a separable algebraic extension, and these are outlined later in the article.
The class of separable extensions is an extremely important one due to the fundamental role it plays in Galois theory. More specifically, a finite degree field extension is Galois if and only if it is both normal and separable.[2] Since algebraic extensions of fields of characteristic zero, and of finite fields, are separable, separability is not an obstacle in most applications of Galois theory.[3][4] For instance, every algebraic (in particular, finite degree) extension of the field of rational numbers is necessarily separable.
Despite the ubiquity of the class of separable extensions in mathematics, its extreme opposite, namely the class of purely inseparable extensions, also occurs quite naturally. An algebraic extension  is a purely inseparable extension if and only if for every
is a purely inseparable extension if and only if for every 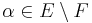 , the minimal polynomial of
, the minimal polynomial of  over F is not a separable polynomial (i.e., does not have distinct roots).[5] For a field F to possess a non-trivial purely inseparable extension, it must necessarily be an infinite field of prime characteristic (i.e. specifically, imperfect), since any algebraic extension of a perfect field is necessarily separable.[6]
over F is not a separable polynomial (i.e., does not have distinct roots).[5] For a field F to possess a non-trivial purely inseparable extension, it must necessarily be an infinite field of prime characteristic (i.e. specifically, imperfect), since any algebraic extension of a perfect field is necessarily separable.[6]
The study of separable extensions in their own right has far-reaching consequences. For instance, consider the result: "If E is a field with the property that every nonconstant polynomial with coefficients in E has a root in E, then E is algebraically closed."[7] Despite its simplicity, it suggests a deeper conjecture: "If  is an algebraic extension and if every nonconstant polynomial with coefficients in F has a root in E, is E algebraically closed?"[8] Although this conjecture is true, most of its known proofs depend on the theory of separable and purely inseparable extensions; for instance, in the case corresponding to the extension
is an algebraic extension and if every nonconstant polynomial with coefficients in F has a root in E, is E algebraically closed?"[8] Although this conjecture is true, most of its known proofs depend on the theory of separable and purely inseparable extensions; for instance, in the case corresponding to the extension  being separable, one known proof involves the use of the primitive element theorem in the context of Galois extensions.[9]
being separable, one known proof involves the use of the primitive element theorem in the context of Galois extensions.[9]
Contents |
Informal discussion
The reader may wish to assume that, in what follows, F is the field of rational, real or complex numbers, unless otherwise stated.
An arbitrary polynomial f with coefficients in some field F is said to have distinct roots if and only if it has deg(f) roots in some extension field  . For instance, the polynomial g(X)=X2+1 with real coefficients has precisely deg(g)=2 roots in the complex plane; namely the imaginary unit i, and its additive inverse −i, and hence does have distinct roots. On the other hand, the polynomial h(X)=(X−2)2 with real coefficients does not have distinct roots; only 2 can be a root of this polynomial in the complex plane and hence it has only one, and not deg(f)=2 roots.
. For instance, the polynomial g(X)=X2+1 with real coefficients has precisely deg(g)=2 roots in the complex plane; namely the imaginary unit i, and its additive inverse −i, and hence does have distinct roots. On the other hand, the polynomial h(X)=(X−2)2 with real coefficients does not have distinct roots; only 2 can be a root of this polynomial in the complex plane and hence it has only one, and not deg(f)=2 roots.
In general, it can be shown that the polynomial f with coefficients in F has distinct roots if and only if for any extension field  , and any
, and any 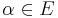 ,
, 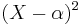 does not divide f in E[X]. For instance, in the above paragraph, one observes that g has distinct roots and indeed g(X)=(X+i)(X−i) in the complex plane (and hence cannot have any factor of the form
does not divide f in E[X]. For instance, in the above paragraph, one observes that g has distinct roots and indeed g(X)=(X+i)(X−i) in the complex plane (and hence cannot have any factor of the form 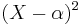 for any
for any  in the complex plane). On the other hand, h does not have distinct roots and indeed, h(X)=(X−2)2 in the complex plane (and hence does have a factor of the form
in the complex plane). On the other hand, h does not have distinct roots and indeed, h(X)=(X−2)2 in the complex plane (and hence does have a factor of the form 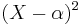 for
for 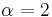 ).
).
Although an arbitrary polynomial with rational or real coefficients may not have distinct roots, it is natural to ask at this stage whether or not there exists an irreducible polynomial with rational or real coefficients that does not have distinct roots. The polynomial h(X)=(X−2)2 does not have distinct roots but it is not irreducible as it has a non-trivial factor (X−2). In fact, it is true that there is no irreducible polynomial with rational or real coefficients that does not have distinct roots; in the language of field theory, every algebraic extension of 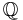 or
or  is separable and hence both of these fields are perfect.
is separable and hence both of these fields are perfect.
Separable and inseparable polynomials
A polynomial f in F[X] is a separable polynomial if and only if every irreducible factor of f in F[X] has distinct roots.[10] The separability of a polynomial depends on the field in which its coefficients are considered to lie; for instance, if g is an inseparable polynomial in F[X], and one considers a splitting field, E, for g over F, g is necessarily separable in E[X] since an arbitrary irreducible factor of g in E[X] is linear and hence has distinct roots.[11] Despite this, a separable polynomial h in F[X] must necessarily be separable over every extension field of F.[12]
Let f in F[X] be an irreducible polynomial and f' its formal derivative. Then the following are equivalent conditions for f to be separable; that is, to have distinct roots:
- If
 and
and 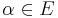 , then
, then 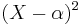 does not divide f in E[X].[13]
does not divide f in E[X].[13] - There exsits
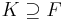 such that f has deg(f) roots in K.[13]
such that f has deg(f) roots in K.[13] - f and f' do not have a common root in any extension field of F.[14]
- f' is not the zero polynomial.[15]
By the last condition above, if an irreducible polynomial does not have distinct roots, its derivative must be zero. Since the formal derivative of a positive degree polynomial can be zero only if the field has prime characteristic, for an irreducible polynomial to not have distinct roots its coefficients must lie in a field of prime characteristic. More generally, if an irreducible (non-zero) polynomial f in F[X] does not have distinct roots, not only must the characteristic of F be a (non-zero) prime number p, but also f(X)=g(Xp) for some irreducible polynomial g in F[X].[16] By repeated application of this property, it follows that in fact, 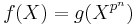 for a non-negative integer n and some separable irreducible polynomial g in F[X] (where F is assumed to have prime characteristic p).[17]
for a non-negative integer n and some separable irreducible polynomial g in F[X] (where F is assumed to have prime characteristic p).[17]
By the property noted in the above paragraph, if f is an irreducible (non-zero) polynomial with coefficients in the field F of prime characteristic p, and does not have distinct roots, it is possible to write f(X)=g(Xp). Furthermore, if 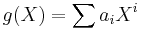 , and if the Frobenius endomorphism of F is an automorphism, g may be written as
, and if the Frobenius endomorphism of F is an automorphism, g may be written as 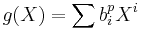 , and in particular,
, and in particular, 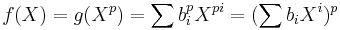 ; a contradiction of the irreducibility of f. Therefore, if F[X] possesses an inseparable irreducible (non-zero) polynomial, then the Frobenius endomorphism of F cannot be an automorphism (where F is assumed to have prime characteristic p).[18]
; a contradiction of the irreducibility of f. Therefore, if F[X] possesses an inseparable irreducible (non-zero) polynomial, then the Frobenius endomorphism of F cannot be an automorphism (where F is assumed to have prime characteristic p).[18]
If K is a finite field of prime characteristic p, and if X is an indeterminant, then the field of rational functions over K, K(X), is necessarily imperfect. Furthermore, the polynomial f(Y)=Yp−X is inseparable.[19] (To see this, note that there is some extension field 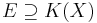 in which f has a root
in which f has a root  ; necessarily,
; necessarily, 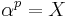 in E. Therefore, working over E,
in E. Therefore, working over E, 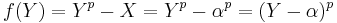 (the final equality in the sequence follows from freshman's dream), and f does not have distinct roots.) More generally, if F is any field of (non-zero) prime characteristic for which the Frobenius endomorphism is not an automorphism, F possesses an inseparable algebraic extension.[20]
(the final equality in the sequence follows from freshman's dream), and f does not have distinct roots.) More generally, if F is any field of (non-zero) prime characteristic for which the Frobenius endomorphism is not an automorphism, F possesses an inseparable algebraic extension.[20]
A field F is perfect if and only if all of its algebraic extensions are separable (in fact, all algebraic extensions of F are separable if and only if all finite degree extensions of F are separable). By the argument outlined in the above paragraphs, it follows that F is perfect if and only if F has characteristic zero, or F has (non-zero) prime characteristic p and the Frobenius endomorphism of F is an automorphism.
Properties
- If
 is an algebraic field extension, and if
is an algebraic field extension, and if 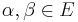 are separable over F, then
are separable over F, then 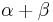 and
and 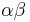 are separable over F. In particular, the set of all elements in E separable over F forms a field.[21]
are separable over F. In particular, the set of all elements in E separable over F forms a field.[21] - If
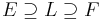 is such that
is such that 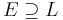 and
and 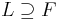 are separable extensions, then
are separable extensions, then  is separable.[22] Conversely, if
is separable.[22] Conversely, if  is a separable algebraic extension, and if L is any intermediate field, then
is a separable algebraic extension, and if L is any intermediate field, then 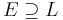 and
and 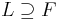 are separable extensions.[23]
are separable extensions.[23] - If
 is a finite degree separable extension, then it has a primitive element; i.e., there exists
is a finite degree separable extension, then it has a primitive element; i.e., there exists 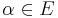 with
with ![E=F[\alpha]](/2012-wikipedia_en_all_nopic_01_2012/I/55e2f89d43e3631374df81f20a13af90.png) . This fact is also known as the primitive element theorem or Artin's theorem on primitive elements.
. This fact is also known as the primitive element theorem or Artin's theorem on primitive elements.
Purely inseparable extensions
An algebraic extension  is a purely inseparable extension if and only if for every
is a purely inseparable extension if and only if for every 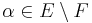 , the minimal polynomial of
, the minimal polynomial of  over F is not a separable polynomial.[24] If F is any field, the trivial extension
over F is not a separable polynomial.[24] If F is any field, the trivial extension 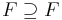 is purely inseparable; for the field F to possess a non-trivial purely inseparable extension, it must be imperfect as outlined in the above section.
is purely inseparable; for the field F to possess a non-trivial purely inseparable extension, it must be imperfect as outlined in the above section.
Several equivalent and more concrete definitions for the notion of a purely inseparable extension are known. If  is an algebraic extension with (non-zero) prime characteristic p, then the following are equivalent[25]:
is an algebraic extension with (non-zero) prime characteristic p, then the following are equivalent[25]:
1. E is purely inseparable over F
2. For each element 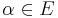 , there exists
, there exists 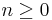 such that
such that 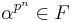 .
.
3. Each element of E has minimal polynomial over F of the form 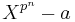 for some integer
for some integer 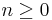 and some element
and some element 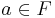 .
.
It follows from the above equivalent characterizations that if ![E=F[\alpha]](/2012-wikipedia_en_all_nopic_01_2012/I/55e2f89d43e3631374df81f20a13af90.png) (for F a field of prime characteristic) such that
(for F a field of prime characteristic) such that 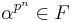 for some integer
for some integer 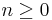 , then E is purely inseparable over F.[26] (To see this, note that the set of all x such that
, then E is purely inseparable over F.[26] (To see this, note that the set of all x such that 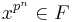 for some
for some 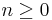 forms a field; since this field contains both
forms a field; since this field contains both  and F, it must be E, and by condition 2 above,
and F, it must be E, and by condition 2 above,  must be purely inseparable.)
must be purely inseparable.)
If F is an imperfect field of prime characteristic p, choose 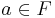 such that a is not a pth power in F, and let f(X)=Xp−a. Then f has no root in F, and so if E is a splitting field for f over F, it is possible to choose
such that a is not a pth power in F, and let f(X)=Xp−a. Then f has no root in F, and so if E is a splitting field for f over F, it is possible to choose  with
with 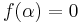 . In particular,
. In particular, 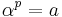 and by the property stated in the paragraph directly above, it follows that
and by the property stated in the paragraph directly above, it follows that ![F[\alpha]\supseteq F](/2012-wikipedia_en_all_nopic_01_2012/I/9e7f92ac885935e9641a0fd687802a2b.png) is a non-trivial purely inseparable extension (in fact,
is a non-trivial purely inseparable extension (in fact, ![E=F[\alpha]](/2012-wikipedia_en_all_nopic_01_2012/I/55e2f89d43e3631374df81f20a13af90.png) , and so
, and so  is automatically a purely inseparable extension).[27]
is automatically a purely inseparable extension).[27]
Purely inseparable extensions do occur naturally; for example, they occur in algebraic geometry over fields of prime characteristic. If K is a field of characteristic p, and if V is an algebraic variety over K of dimension greater than zero, the function field K(V) is a purely inseparable extension over the subfield K(V)p of pth powers (this follows from condition 2 above). Such extensions occur in the context of multiplication by p on an elliptic curve over a finite field of characteristic p.
Properties
- If the characteristic of a field F is a (non-zero) prime number p, and if
 is a purely inseparable extension, then if
is a purely inseparable extension, then if 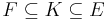 , K is purely inseparable over F and E is purely inseparable over K. Furthermore, if [E : F] is finite, then it is a power of p, the characteristic of F.[28]
, K is purely inseparable over F and E is purely inseparable over K. Furthermore, if [E : F] is finite, then it is a power of p, the characteristic of F.[28] - Conversely, if
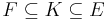 is such that
is such that 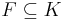 and
and 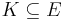 are purely inseparable extensions, then E is purely inseparable over F.[29]
are purely inseparable extensions, then E is purely inseparable over F.[29] - An algebraic extension
 is an inseparable extension if and only if there is some
is an inseparable extension if and only if there is some 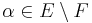 such that the minimal polynomial of
such that the minimal polynomial of  over F is not a separable polynomial (i.e., an algebraic extension is inseparable if and only if it is not separable; note, however, that an inseparable extension is not the same thing as a purely inseparable extension). If
over F is not a separable polynomial (i.e., an algebraic extension is inseparable if and only if it is not separable; note, however, that an inseparable extension is not the same thing as a purely inseparable extension). If  is a finite degree non-trivial inseparable extension, then [E : F] is necessarily divisible by the characteristic of F.[30]
is a finite degree non-trivial inseparable extension, then [E : F] is necessarily divisible by the characteristic of F.[30] - If
 is a finite degree normal extension, and if
is a finite degree normal extension, and if 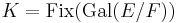 , then K is purely inseparable over F and E is separable over K.[31]
, then K is purely inseparable over F and E is separable over K.[31]
Separable extensions within algebraic extensions
Separable extensions occur quite naturally within arbitrary algebraic field extensions. More specifically, if  is an algebraic extension and if
is an algebraic extension and if 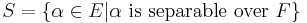 , then S is the unique intermediate field that is separable over F and over which E is purely inseparable.[32] If
, then S is the unique intermediate field that is separable over F and over which E is purely inseparable.[32] If  is a finite degree extension, the degree [S : F] is referred to as the separable part of the degree of the extension
is a finite degree extension, the degree [S : F] is referred to as the separable part of the degree of the extension  (or the separable degree of E/F), and is often denoted by [E : F]sep or [E : F]s.[33] The inseparable degree of E/F is the quotient of the degree by the separable degree. When the characteristic of F is p > 0, it is a power of p.[34] Since the extension
(or the separable degree of E/F), and is often denoted by [E : F]sep or [E : F]s.[33] The inseparable degree of E/F is the quotient of the degree by the separable degree. When the characteristic of F is p > 0, it is a power of p.[34] Since the extension  is separable if and only if
is separable if and only if 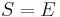 , it follows that for separable extensions, [E : F]=[E : F]sep, and conversly. If
, it follows that for separable extensions, [E : F]=[E : F]sep, and conversly. If  is not separable (i.e., inseparable), then [E : F]sep is necessarily a non-trivial divisor of [E : F], and the quotient is necessarily a power of the characteristic of F.[35]
is not separable (i.e., inseparable), then [E : F]sep is necessarily a non-trivial divisor of [E : F], and the quotient is necessarily a power of the characteristic of F.[35]
On the other hand, an arbitrary algebraic extension  may not possess an intermediate extension K that is purely inseparable over F and over which E is separable (however, such an intermediate extension does exist when
may not possess an intermediate extension K that is purely inseparable over F and over which E is separable (however, such an intermediate extension does exist when  is a finite degree normal extension (in this case, K can be the fixed field of the Galois group of E over F)). If such an intermediate extension does exist, and if [E : F] is finite, then if S is defined as in the previous paragraph, [E : F]sep=[S : F]=[E : K].[36] One known proof of this result depends on the primitive element theorem, but there does exist a proof of this result independent of the primitive element theorem (both proofs use the fact that if
is a finite degree normal extension (in this case, K can be the fixed field of the Galois group of E over F)). If such an intermediate extension does exist, and if [E : F] is finite, then if S is defined as in the previous paragraph, [E : F]sep=[S : F]=[E : K].[36] One known proof of this result depends on the primitive element theorem, but there does exist a proof of this result independent of the primitive element theorem (both proofs use the fact that if 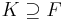 is a purely inseparable extension, and if f in F[X] is a separable irreducible polynomial, then f remains irreducible in K[X][37]). The equality above ([E : F]sep=[S : F]=[E : K]) may be used to prove that if
is a purely inseparable extension, and if f in F[X] is a separable irreducible polynomial, then f remains irreducible in K[X][37]). The equality above ([E : F]sep=[S : F]=[E : K]) may be used to prove that if 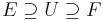 is such that [E : F] is finite, then [E : F]sep=[E : U]sep[U : F]sep.[38]
is such that [E : F] is finite, then [E : F]sep=[E : U]sep[U : F]sep.[38]
If F is any field, the separable closure Fsep of F is the field of all elements in the algebraic closure of F that are separable over F. The separable closure of F is useful in that Galois theory may be carried out within it. Of course, if F is perfect, then the separable closure of F is precisely its algebraic closure (in particular, the notion of a separable closure is only interesting in the context of imperfect fields).
The definition of separable non-algebraic extension fields
Although many important applications of the theory of separable extensions stem from the context of algebraic field extensions, there are important instances in mathematics where it is profitable to study (not necessarily algebraic) separable field extensions.
Let 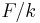 be a field extension and let p be the characteristic exponent of
be a field extension and let p be the characteristic exponent of  .[39] For any field extension L of k, we write
.[39] For any field extension L of k, we write 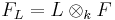 (cf. Tensor product of fields.) Then F is said to be separable over
(cf. Tensor product of fields.) Then F is said to be separable over  if the following equivalent conditions are met:
if the following equivalent conditions are met:
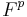 and
and  are linearly disjoint over
are linearly disjoint over 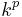
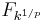 is reduced.
is reduced.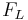 is reduced for all field extensions L of k.
is reduced for all field extensions L of k.
(In other words, F is separable over k if F is a separable k-algebra.)
Suppose there is some field extension L of k such that 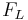 is a domain. Then
is a domain. Then  is separable over k if and only if the field of fractions of
is separable over k if and only if the field of fractions of 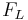 is separable over L.
is separable over L.
An algebraic element of F is said to be separable over  if its minimal polynomial is separable. If
if its minimal polynomial is separable. If 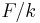 is an algebraic extension, then the following are equivalent.
is an algebraic extension, then the following are equivalent.
- F is separable over k.
- F consists of elements that are separable over k.
- Every subextension of F/k is separable.
- Every finite subextension of F/k is separable.
If 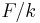 is finite extension, then the following are equivalent.
is finite extension, then the following are equivalent.
- (i) F is separable over k.
- (ii)
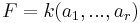 where
where  are separable over k.
are separable over k. - (iii) In (ii), one can take
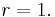
- (iv) For some very large field
 , there are precisely
, there are precisely ![[F�: k]](/2012-wikipedia_en_all_nopic_01_2012/I/640c28946039b98be9ee191a4772aeb5.png) k-isomorphisms from
k-isomorphisms from  to
to  .
.
In the above, (iii) is known as the primitive element theorem.
Fix the algebraic closure 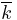 , and denote by
, and denote by 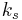 the set of all elements of
the set of all elements of 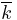 that are separable over k.
that are separable over k. 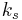 is then separable algebraic over k and any separable algebraic subextension of
is then separable algebraic over k and any separable algebraic subextension of 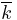 is contaiend in
is contaiend in 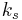 ; it is called the separable closure of k (inside
; it is called the separable closure of k (inside 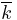 ).
). 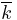 is then purely inseparable over
is then purely inseparable over 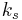 . Put in another way, k is perfect if and only if
. Put in another way, k is perfect if and only if 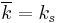 .
.
Differential criteria
The separability can be studied with the aid of derivations and Kähler differentials. Let  be a finitely generated field extension of a field
be a finitely generated field extension of a field  . Then
. Then
where the equality holds if and only if F is separable over k.
In particular, if 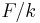 is an algebraic extension, then
is an algebraic extension, then 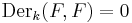 if and only if
if and only if 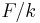 is separable.
is separable.
Let 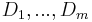 be a basis of
be a basis of 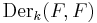 and
and 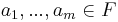 . Then
. Then  is separable algebraic over
is separable algebraic over 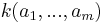 if and only if the matrix
if and only if the matrix 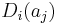 is invertible. In particular, when
is invertible. In particular, when 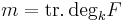 ,
, 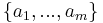 above is called the separating transcendence basis.
above is called the separating transcendence basis.
See also
- Separable polynomial
- Perfect field
- Primitive element theorem
- Normal extension
- Galois extension
- Algebraic closure
- Derivation
Notes
- ^ Isaacs, p. 281
- ^ Isaacs, Theorem 18.13, p. 282
- ^ Isaacs, Theorem 18.11, p. 281
- ^ Isaacs, p. 293
- ^ Isaacs, p. 298
- ^ Isaacs, Theorem 18.11, p. 281
- ^ Isaacs, Theorem 19.22, p. 303
- ^ Isaacs, p. 269
- ^ Isaacs, Theorem 19.22, p. 303
- ^ Isaacs, p. 280
- ^ Isaacs, p. 281
- ^ Isaacs, Lemma 18.10, p. 281
- ^ a b Isaacs, Lemma 18.7, p. 280
- ^ Isaacs, Theorem 19.4, p. 295
- ^ Isaacs, Corollary 19.5, p. 296
- ^ Isaacs, Corollary 19.6, p. 296
- ^ Isaacs, Corollary 19.9, p. 298
- ^ Isaacs, Theorem 19.7, p. 297
- ^ Isaacs, p. 281
- ^ Isaacs, p. 299
- ^ Isaacs, Lemma 19.15, p. 300
- ^ Isaacs, Corollary 19.17, p. 301
- ^ Isaacs, Corollary 18.12, p. 281
- ^ Isaacs, p. 298
- ^ Isaacs, Theorem 19.10, p. 298
- ^ Isaacs, Corollary 19.11, p. 298
- ^ Isaacs, p. 299
- ^ Isaacs, Corollary 19.12, p. 299
- ^ Isaacs, Corollary 19.13, p. 300
- ^ Isaacs, Corollary 19.16, p. 301
- ^ Isaacs, Theorem 19.18, p. 301
- ^ Isaacs, Theorem 19.14, p. 300
- ^ Isaacs, p. 302
- ^ Lang 2002, Corollary V.6.2
- ^ Isaacs, p. 302
- ^ Isaacs, Theorem 19.19, p. 302
- ^ Isaacs, Lemma 19.20, p. 302
- ^ Isaacs, Corollary 19.21, p. 303
- ^ The characteristic exponent of k is 1 if k has characteristic zero; otherwise, it is the characteristic of k.
References
- Borel, A. Linear algebraic groups, 2nd ed.
- P.M. Cohn (2003). Basic algebra
- I. Martin Isaacs (1993). Algebra, a graduate course (1st ed.). Brooks/Cole Publishing Company. ISBN 0-534-19002-2.
- M. Nagata (1985). Commutative field theory: new edition, Shokado. (Japanese) [1]
- Silverman, Joseph (1993). The Arithmetic of Elliptic Curves. Springer. ISBN 0-387-96203-4.
External links
- Hazewinkel, Michiel, ed. (2001), "separable extension of a field k", Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=s/s084470